El siglo de la fraternidad 9 - Construcción

Chico Buarque

A partir de un escenario constructivista surge todo lo humano.

Cada ser humano tiene necesidades que debe atender para mantenerse con vida, ya sean bienes materiales, espacios físicos, espacios de relacionamiento, afectos o emociones. Adolece de muchas cosas que necesita para el día a día para la vida misma, esas necesidades lo hacen ir en una búsqueda permanente de disponibilidades que satisfagan esas necesidades. Es cuando en su camino se encuentra con otros preocupados por la misma empresa y así conoce lo común que no es otra cosa que una necesidad común que para satisfacerla deviene en una búsqueda común.

Así, reconociendo en el otro, lo común que lo aglutina es que empieza a reunirse torno a las disponibilidades que estén a su alcance. Por lo que el colectivo surge a partir del entorno. Hombres y mujeres, concurren en común unión hacia las disponibilidades y de esa manera se organizan y se conforman en torno a algo que no les pertenece, sino que está allá afuera y que es capaz de satisfacer esas necesidades comunes.

Por lo que la comunión surge a partir del entorno o mejor dicho a partir de la diferencia con este. El entorno posee lo que la comunidad adolece, esa es la diferencia. Pero ese entorno para existir debe ser puesto de manifiesto por quién lo demande, quién lo entorne. La relación que se establece entre entorno y comunidad es lo que se mencionaba en el primer capítulo como biopolítica, es la demanda por la vida y es justamente esa diferencia la que pondrá en movimiento el intercambio de flujos.

Amó aquella vez como si fuese última
Besó a su mujer como si fuese última
Y a cada hijo suyo cual si fuese el único
Y atravesó la calle con su paso tímido
Subió a la construcción como si fuese máquina
Alzó en el balcón cuatro paredes sólidas
Ladrillo con ladrillo en un diseño mágico
Sus ojos embotados de cemento y lágrimas
Sentóse a descansar como si fuese sábado
Comió su pan con queso cual si fuese un príncipe
Bebió y sollozó como si fuese un náufrago
Danzó y se rió como si oyese música
Y tropezó en el cielo con su paso alcohólico
Y flotó por el aire cual si fuese un pájaro
Y terminó en el suelo como un bulto fláccido
Y agonizó en el medio del paseo público
Murió a contramano entorpeciendo el tránsito

En un primer escenario podemos reconocer a los actores que se congregan en torno a una necesidad común que buscan satisfacerla en torno a una determinada disponibilidad que buscan  y encuentran. Que posee lo que ellos necesitan por eso interpelan al entorno en una demanda común por los flujos que necesitan para subsistir y de esta forma adquieren una identidad.

Lo común de esta manera se configura como lo aglutinante y como la matriz que les da su identidad y a su vez hace las veces de piel social. Lo común les confiere una coherencia estructural que surge entre los agentes entre sí además de una coherencia de la estructura social emergente en su diferencia con el entorno. Actúa de esta manera como una matriz que va generando su propio contenido y a media que lo genera se va autogenerando.

Este proceso se podría describir también como totalidades de la que emergen totalidades que a su vez se autogeneran, van heredando propiedades de las anteriores emergencia marcando una resiliencia que queda como una memoria de red, o herencia.

Amó aquella vez como si fuese el último
Besó a su mujer como si fuese única
Y a cada hijo suyo cual si fuese el pródigo
Y atravesó la calle con su paso alcohólico
Subió a la construcción como si fuese sólida
Alzó en el balcón cuatro paredes mágicas
Ladrillo con ladrillo en un diseño lógico
Sus ojos embotados de cemento y tránsito
Sentose a descansar como si fuese un príncipe
Comió su pan con queso cual si fuese el máximo
Bebió y sollozó como si fuese máquina
Danzó y se rió como si fuese el próximo
Y tropezó en el cielo cual si oyese música
Y flotó por el aire cual si fuese sábado
Y terminó en el suelo como un bulto tímido
Agonizó en el medio del paseo náufrago
Murió a contramano entorpeciendo el público

En un segundo escenario vemos que todo es móvil, tanto lo emergido, como el entorno, como la diferencia que se establece entre ambos. Todo evoluciona en el tiempo haciendo que desde la emergencia las necesidades, la concurrencia y la búsqueda están en permanente cambio y subsisten siempre.

No hay sujetos, ya que nada permanece fijo, todo evoluciona en algún sentido por lo que no se puede tampoco hablar de objetos determinado que interactúan atómicamente, sino que las singularidades van conformando la multiplicidad en la medida en que se vayan incorporándose a lo emergido

Amó aquella vez como si fuese máquina
Besó a su mujer como si fuese lógico
Alzó en el balcón cuatro paredes flácidas
Sentose a descansar como si fuese un pájaro
Y flotó en el aire cual si fuese un príncipe
Y terminó en el suelo como un bulto alcohólico
Murió a contramano entorpeciendo el sábado

El tercer escenario que se debe observar es la diferencia entre emergencia y entorno, responsable de que entre ambos haya un intercambio. La diferencia es una verdadera diferencia de potencial, en donde los flujos se de dirigen desde el mayor potencial , el entorno para asistir las necesidades de la emergencia, repartiéndose hacia todo su interior de acuerdo a una hipótesis ergódica, esto es, que cada agente tenga la misma probabilidad de cubrir sus necesidades a partir del suministro esos flujos.

Por ese pan de comer y el suelo para dormir
Registro para nacer, permiso para reír
Por dejarme respirar y por dejarme existir
Dios le pague

Un cuarto escenario se establece cuando miramos la emergencia como tal, en relación con el entorno. En este caso las singularidades que lo conforman, los agentes, son considerados semejantes estadísticamente, ya que cada uno tiene las mismas probabilidades de recibir los recursos que necesite de acuerdo a la hipótesis ergódica.

Para ello deberá se capaz de movilizarse y coordinarse interiormente dentro de la emergencia, a fin de que el colectivo como conjunto pueda interactuar con el entorno de la forma mas coordinada, favoreciendo la conducción de los flujos (ley constructal), y acortando los tiempos de respuesta ante alguna conmoción provocada por el entorno.

La similitud entre agentes, a partir del reconocimiento y la confianza aporta para que la coordinación dentro de la emergencia sea más simple

Por esa capa de grasa que tenemos que beber
Por ese humo desgracia que tenemos que toser
Por los andamios de gente para subir y caer
Dios le pague

El quinto y último escenario donde se debe posar la mirada es el escenario total donde encontramos que nuestra emergencia no interactúa sola con el entorno, que otras emergencias, similares a esta, también lo hacen y que pese a que por distintas razones se hayan conformado en distintas emergencias, aún poseen mucho en común lo que posibilita, a su vez, un intercambio horizontal entre emergencia y emergencia.

Por esas vidas que un día nos van a escupir
y por las moscas y besos que nos vendrán a cubrir
y por la calma postrera que al fin nos va a redimir
Dios le pague

Como se podrá apreciar esta escena es muy compleja ya que varía en el espacio y en el tiempo, y no desde una linealidad sino desde un proceso que permanente se abre nuevas dimensiones.

Daniel Viglietti Construcción - VOZ REBELDE PERU

Mercedes- Tejada - Calle 13

Un niño en la calle

El siglo de la fraternidad 8-Fractales, Power Laws y jerarquías –segunda parte

A satirical drawing from 1811 of the 'Pigeon Holes' that flanked the upper gallery at Covent Garden

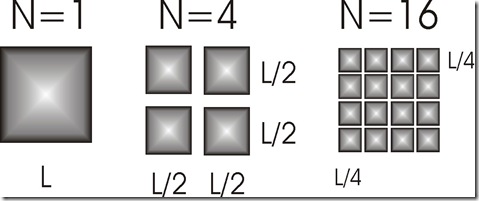
Hasta aquí tratamos de establecer una relación entre las PZM y los fractales. Definimos la dimensión fractal como una constante de proporcionalidad que nos posibilitaba el cambio de escala desde los múltiples casos diversos y dispersos para llegar a los casos más frecuentes, que pese a ser más populosos, son menos diversos.

Podemos entonces conceptuar a las PZM como una distribución que establece un sentido evolutivo desde lo mas frecuente, lo mas concurrido, a lo menos frecuentado, lo menos ocurrente, o su sentido inverso, que se podría describir como una forma fractal que se autogenera a partir de una reproducción de un mismo proceso divergente.

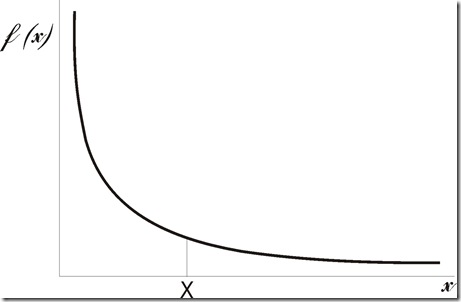
¿Pero qué significan sus ejes de coordenadas? El eje de las x, el eje horizontal, describe la diversidad, las posibles formas disponibles en que las se pueden organizar las y. El otro eje significa la cantidad de casos que tenemos cada x, la frecuencia con que ocurre x, y que luego de ordenarse se distribuirán de una forma particular que va desde una gran variedad de casos distintos con frecuencias de repeticiones muy escasas, al caso totalmente opuesto, grandes conglomerados reunidos alrededor de una muy escasa diversidad.

¿Qué es lo fijo y que es lo móvil de este gráfico? Si el eje de las x representa la diversidad de casos posibles, este dato estará condicionado por el contexto, habrá una determinada diversidad de casos posibles, el eje de las x estará así restringido, en un principio, a las disponibilidades que da el sistema. Representa la disponibilidad que ofrece la naturaleza ante las necesidades de los agentes. Esas disponibilidades son siempre finitas para esos agentes, dado que ellos se constituyen a partir de esos recursos que toman del entorno. Por lo que los agentes se yerguen en base a las disponibilidades que les ofrece la naturaleza y ante esta oferta dada ellos eligen donde posicionarse, y esta restringida distribución de necesidades en base a las posibles disponibilidades hace que el sistema se apile hacia un lado estableciendo una distribución de una forma muy desproporcionada. Recordemos que estamos en un espacio tiempo todavía matriarcal, pre edípico, donde todavía no se ha constituido el sistema económico, donde de lo que hay, hay de todo y en abundancia.

En este sistema los recursos están disponibles de una manera pre determinada (eje de las x) y fluyen libremente para cubrir las necesidades de los agentes que a su vez se agrupan en base a conglomerados de diferentes magnitudes de acuerdo a la disponibilidad de la que se trate. Y aquí viene el problema.

Si, como se vio en el primer capítulo, lo social se instituía en base a lo común, acá vemos que lo común (la totalidad de las disposibilidades ofrecidas al conjunto de agentes a lo largo del eje de las x) no tiene la menor posibilidad de distribuirse equitativamente dado que no tiene nisgún simetría de ningún tipo en su diversidad. ¿Cómo sería posible entonces distribuir lo común; finito y cuantificado en base una dispersión determinada, entre una población de agentes demandantes condicionados por sus necesidades materiales?

 

Con lo primero que nos encontramos es con una distribución que no es ni pareja, ni equitativa, ni aleatoria, ni simétrica y a partir de este dato de la realidad nuestra necesidades reales se deben adaptar a las disponibilidades realmente existentes. Esto de por sí no es muy preocupante luego de miles de años de selección natural. Somos lo que somos en base a las posibilidades de la disponibilidad de nuestro entorno. Estamos constituidos en base a esas disponibilidades. Acaso podríamos sobrevivir en una atmósfera sin oxígeno, tal vez sí pero sería muy difícil.

Foto de acá

Esta idea se podría conceptializar como un casillero de cartas a donde llega la correspondencia de una determinada manera, en donde algunos poseen mucha correspondencia, otros menos y algunos no tienen nada. Sin embargo al ver la foto del casillero solemos obviar que esa distribución está en concordancia con su destinatario, dado que se ubica en el buzón en base a un determinado destinatario acorde a la “necesidad” de correspondencia del dueño del casillero, por lo que en definitiva no importa la forma en que la correspondencia se distribuya en los casilleros sino la necesidad de correspondencia con sus destinatarios. Hay una relación directa entre correspondencia y destinatario que establece un flujo de cartas entre los dos que se podría visualizar como un árbol fractal con el tronco en el correo y su copa en casillero de las cartas. Un árbol con copa desproporcionada y caprichosa que estará en concordancia la demanda de envíos que hacen los destinatarios.

 

Desde la óptica  de los constructivistas radicales (Paul Watzlawick, Ernst Von Glasersfeld, Humberto Maturana, etc) esto podría ser analizado como un casillero que se conforma en base a las necesidades de correspondencia de los destinatarios, sin destinatarios el casillero no tendría razón de ser. Sin embargo no se tiene en cuenta la cuestión de la magnitud del número de cartas que hay en cada casillero. Hay una presuposición que la distribución de las cartas es “aleatoria” para todos los casilleros. También Stuark Kaufmann cuando nos habla de una “sopa primordial” a partir de donde evolucionan los sistemas,  en donde los elementos primitivos a partir de los cuales se constituirán se encuentran distribuidos al azar, tampoco nos habla de la distribución relativa.

De lo que no se habla es de la disponibilidad de esos elementos primitivos. Porque una cosa es que la distribución espacial de dicha disponibilidad sea aleatoria, pero esto no quiere decir que las cantidades relativas estén equilibradas.

Estamos constituidos a partir de replicar el cosmos en nuestros cuerpos, como afrima Stefan Widmer. Nuestros cuerpos emergieron y evolucionaron a partir de las disponibilidades realmente existentes en la naturaleza. Nuestros nutrientes tampoco están distribuidos equitativamente, y en consecuencia de esto que necesitamos de unos elementos más que de otros. Con todos los organismos vivos pasa esto, dentro de la alimentación existen algunas sustancias sin las cuales no podríamos vivir, pese a que nuestros organismos solo necesiten trazas de esos elementos, se los denomina justamente oligoelementos, oligo quiere decir poco.

Sin embargo los fractales junto a las distribuciones PZM forman un conjunto de representación que tiene en cuenta no solo la estructura de flujo sino que también la tensión que se produce entre necesidades y disponibilidades, que por otro lado es la causante de los flujos.

 

Esto nos lleva a entender que esa desproporción de demanda de la diversidad para satisfacer las necesidades de los agentes estará en concordancia, también en un principio, con la magnitud de las disponibilidades del entorno. Pero esa necesidad crece en complejidad a medida que el sistema social avanza evolutivamente y a medida que lo hace los humanos logran, mediante el desarrollo de su inteligencia racional, descontruir la complejidad creciente mediante mecanismos que posibilitan, al menos en la fantasía, reducirla.

Ante la curva cruel y fija de disponibilidades, el ser humano solo puede moverse en los espacios permitidos por sus recursos naturales. Ante la falta de alguno, especialmente los más vitales como el agua, corre serios riesgos de supervivencia; sin embargo posee la razón para resolver este tipo de problema sin necesidad de considerar la posibilidad de exención de buena parte de la comunidad como solución fatalista. Ante la carestía, faltantes, defecto de algún recurso es obvio que un sistema social humano deberá reaccionar racionando los escasos recursos en forma equitativa para llegar a la mayor población demandante. Por lo que de esta manera fantástica la razón se opone a la naturaleza. La razón inventa simetrías inexistentes que posibilitan la distribución equitativa de esos recursos naturalmente escasos.

Esto nos lleva a hablar de los flujos. En realidad analizar una curva PZM es una forma de interpretar y ver un problema de una manera orientada a los cambios de escala y a la relación entre número y frecuencia con respecto a diversidad, analizar el mismo problema desde los fractales correspondientes a PZMs es verlo desde otro punto de vista que pone en evidencia el problema de los flujos.

En realidad flujo es la manifestación de un movimiento relativo, algo moviéndose en relación a un marco al que en general se lo mantiene fijo. El árbol fractal es la representación de la traza que realizan esos flujos desde lo mas a lo menos, desde le tronco hasta las hojas (o el sentido inverso). En el caso de los sistemas sociales estos flujos tienen que ver con: a) los recursos materiales que permiten el metabolismo (controlados por el sistema límbico o autónomo del sistema nervioso), b) los flujos emocionales, que tienen que ver con el sistema periféricos y están en relación con las interacciones emocionales que tejen los agentes entre sí, c) y los flujos del lenguaje racional que tienen que ver con los flujos de información que maneja la parte del cerebro que tiene que ver con el neocortex. La complejidad de este sistema de flujos que se establece entre los humanos, que son analizados por las tres capas del sistema nervioso, hace que los vínculos en una red de interacciones humanas se establezcan en capas de complejidad creciente.

En este punto es bueno discriminar entre el modelo propuesto por West et all y el modelo propuesto por la Ley Constructal de Adrián Bejan. Como se vio en el modelo de West se considera a las punteras del arbol, hojas, capilares, alvéolos, como un remate que hace el fractal natural para no seguir reproduciéndose infinitamente. En un determinado punto de la amplificación la regla fractal en la naturaleza este proceso se detiene y genera una puntera que no corresponde a la evolución fractal del árbol y termina ocluyendo su proceso de crecimiento (segundo principio). El modelo de la ley constructal en este sentido es mas explicito dado que comienza su análisis desde este elemento de punta y en esa punta analiza cual es la mejor ecuación de fraccionamiento del fractal para dar como resultado la mejor (en ese punto) relación entre dispersión del flujo y resistencia al avance. Predice, por ejemplo, que el mejor número de fraccionamiento del árbol traqueal para llegar al alvéolo (puntera) es de 29 fracciones, dado que es justamente ese número el que prevé la mejor relación para que el oxígeno pase de su fase gaseosa a la sangre, dato que se corrobora en todo árbol traqueal. En el caso de la cuenca de los ríos, estudia la mejor relación de superficie captora capaz de tributar en una corriente mayor y así todas esas pequeñas punteras desembocan en el cause del río.

Nosotros proponemos un camino intermedio ya que creemos que ambos tienen razón. Desde la óptica de West et all, se parte de un concurrencia en el tronco que se dispersa en un flujo con forma de árbol fractal que se reproduce hasta un determinado punto a que consideran como excepción a la regla y fin de la abstracción (infinita) matemática. El caso de Adrian Bejan realiza el análisis en sentido inverso. Se sitúa en la puntera y analiza allí cómo hacer posible que los flujos provenientes del árbol fractal fluyan hasta ese punto de manera mas fácil y a partir de esa forma primitiva construye el arbol en sentido inverso al grupo West. Pero lo que no tiene en cueta Bejan es que esas condiciones con las que calcula la mejor ecuación de flujo para la puntera es para el momento el punto y las condiciones de entorno del momento en que se haga el análisis. Nadie sabe como hubiesen sido los pulmones en alguna atmósfera mas sulfurosa, por ejemplo, por lo que su conclusión es válida para esta atmósfera que tiene una disponibilidad de CO2 y O2 determinada, y no para otra con mas azufre, por ejemplo. Un modelo está mas centrado en la forma fractal y en las disponibilidades y no resuelve el tema de las punteras, el otro se hace fuerte para resolver las ecuaciones de mecánica de los fluidos pero sin considerar la disponibilidades pasadas y futuras del sistema.

En consecuencia es necesario asociar a nuestro árbol fractal una PZM correspondiente y veremos que, aceptando una mínima concurrencia de las necesidades hacia las disponibilidades,  existe un flujo desde lo mayor a lo menor, desde un centro parcialmente clusterizado hacia una periferia descentralizada.

Esta concurrencia de necesidades dará para muchísimas discusiones pero este tipo de “jerarquía” de las disponibilidades no es propia de los humanos sino es una característica del cosmos y como tal debemos respetarla dado que tiene la lógica restricción material que es necesaria para que los cuerpos puedan subsistir con vida.

Diagrama de concurrencia

 

¿Esto quiere decir que 0 es un Hub? En cierta medida si y en cierta medida no. Cuando hablamos de red distribuida como dimensión fractal o topológica (en las definiciones de Luque y Agea) de una red social humana, no estamos hablando de una red totalmente distribuida con coeficiente de clusterización = 1 sino que hablamos de una red con un grado de distribución (un cc alrededor de 60%) mayor al grado de centralidad que presenta. Esto quiere decir una red que mantiene una proporción de enlaces reales sobre los enlaces posibles del 60% una vez retirado el nodo mas conectado.

 

Escapa al alcance de este trabajo calcular las necesidades de un agente cualquiera (dato que quedaría por corroborarse teóricamente), pero podríamos suponer como válido el Número de Dumbar como número máximo de agentes dentro de una red de interacción directa y seis el máximo grado de separación entre los mismos, ambos surgidos del la constatación empírica. Esto quiere decir que para que los flujos lleguen a un miembro X de una comunidad de interacción directa, dicha comunidad no debería superar el Número de Dumbar de sus miembros ni estar separados unos de otros más que seis saltos, dado que el sistema nervioso humano no podrá manejar (en sus tres niveles de control de flujos) ni un número mayor de miembros, ni una distancia social mayor.

Este dato es una media y se basa en los datos que aporta la naturaleza, no quiere decir que la grafía de todas las redes sociales humanas de interacción directa tengan esta grafía, o que la grafía que presentan sea para toda la eternidad, pero como dicta la Ley constructal tender hacia esta grafía significa facilitar la circulación de los flujos para que esto puedan fluir más fácilmente.

 

Consideraciones:

1                    Hay  nk ramas a nivel k

2                    La paredes de las venas son rígidas, de radios rk

3                    Se conserva el volumen del fluido

4                    El diámetro de los capilares está dado

5                    La potencia de bombeo está minimizada

Conclusiones:

Radio relativo rk largo k escalar con n, y n es el mismo en cada nivel  de ram

1.      Tasa metabólica B =αM.75

2.      Esta regle de escala deviene en muchas otras con aplicaciones diversas.

 

Geoffrey B. West, James H. Brown, Brian J. Enquist, a huge range of body sizes� “A General Model for the Origin of Allometric� Scaling Laws in Biology,”� Science Vol. 276 4 April 1997, p 122� Internal Structure 4/6/06 © Daniel E Whitney� 19

 

Luego de este complejo y abstracto recorrido llegamos a conclusiones sorprendentes, dado que no estamos analizando sistemas biológicos como los descriptos donde la evolución de un diseño tarda muchísimo tiempo, miles de años. Nosotros estamos hablando de organizaciones sociales entre seres humanos.

Para entender lo que queremos decir nos debemos concentrar en el Δx que habíamos ampliado de nuestra curva Power Law.

 

 

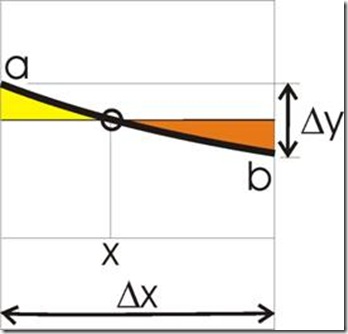
A lo largo de toda la curva  (de cualquier Δx) para cada Δx encontraremos un Δy >0, eso es típico de la curva y nos habla en qué punto de la concurrencia de la curva nos encontramos con el Δx. A mayor Δy, estaremos en la porción de la curva donde las necesidades son mayores para cada Δx, a medida que Δy decrece la curva se hace mas pareja y la necesidades se hace mas semejantes.

Por lo que para cada b tendremos un a con mayor concurrencia, esto quiere decir que son mayores las necesidades en a que en b y esa diferencia de necesidades será la responsable de la estabilidad de mi Δx.

Tampoco vemos la forma de estabilizar equitativamente esta distribución ya que no existe simetría posible, o más precisamente a mayor Δy menores serán las posibilidades de establecer repartos equitativos. Esto hace que los flujos sean mayores del lado de a que del lado de b, dada la desigualdad de a con b, por lo que el sistema deberá compensar esa diferencia vehiculizando con mayor facilidad los flujos cercanos a a que a los de b, por lo que la actividad del lado de a de la pared del diferencial será mucho mas activa que la de b. Todo esto sin dejar de tener en cuenta que esto es solo una porción de la curva para una condición de disponibilidad dada y en un tiempo dado.

Como conclusión y transportados al diagrama de árbol vemos que la parte mas solicitada (compartida por mas usuarios) de Δx es la parte correspondiente al tronco (el lado de a), la parte mas libre es su lado opuesto, donde las ramas son menos concurridas, menos solicitadas por lo que están mas libres. Por eso para cada Δx podemos considerar una parte del follaje del árbol en donde el margen derecho del Δx, correspondiente a la parte mas cercana a las punteras de árbol, son las partes mas libres del follaje y  podemos tener PZM diversas que compartan la misma porción Δx e inclusive dentro de la misma PZM podríamos establecer categorías tales que el Δy posibilite una determinada o pactada similitud entre agentes.

Por eso para cada Δx tendremos una porción a de la curva mas concurrida y solicitada y por ende rigidizada y una porción b de la curva, mas novel en donde los agentes están mas libres, incluso si dividiéramos el Δx en dos mitades iguales  la mitad que contiene a a será mas dispar que la porción que quede del lado de b por la propia forma de la curva, del lado de b las similitudes son mayores que del lado de a, Esto se repite a lo largo de toda la curva y para cualquier porción.

Entonces es propicio traer aquello que citábamos de  Peter Winiwarter en el capítulo 3 referente a su figura que llamaba jerarquía de tres niveles

Figura. La jerarquía de tres niveles de la distribución de Pareto-Zipf-Mandelbrot PZM: unidades procesamiento locales (pequeños puntos), clases de unidades de procesamiento (círculos punteados) y sistema de interacción global (círculo grueso)

La porción cercana a a de nuestro Δx representa la clase que contiene lo que él llama unidades procesamiento locales que son los agentes mas libre del lado derecho del Δx. Este dispositivo se replica fractalmente y en conjunto conforman sistema. Por motivos de grados de libertad del árbol y de la curva las unidades de procesamiento locales, los agentes, tienen mayor posibilidad de movilidad que las porciones mas cercana al tronco del árbol. Esta rigidez es creciente y se incrementa hasta ser casi inamovible, ya que el sistema solo se interrelaciona con otros sistemas y con el entorno, por lo que solo cambiará cuando un factor exógeno así lo determine.

Entonces quedan claras las dos solicitudes que hacen ambos modelos al sistema. Para sistemas establecidos con entornos estabilizados (ley constructal), éste evolucionará internamente en la dirección que los flujos lleguen de la manera mas fácil hasta los agentes. Para entornos cambiantes, el árbol no dudará en dar nuevas ramas extendiendo su fractal mas allá de la suerte que corran los agentes mas extremos.

Si de este capítulo queda clara esta idea, es suficiente por ahora. En el próximo capítulo analizaremos cada parte de la curva aplicándola específicamente para un sistema social de interacción directa. La fraternidad es la forma que toma la clase para que hace posible que lleguen los flujos a los puntos mas extremos de la comunidad de una manera sustentable en el tiempo. Pero eso en el próximo capítulo.

El siglo de la fraternidad 8-Fractales, Power Laws y jerarquías

En este capítulo intentaremos mostrar como se relacionan las redes sociales con las redes de libre escala a través de las distribuciones PZM descriptas en el capítulo 3. Este tipo de distribuciones son muy interesantes debido que se encuentran por doquier en la naturaleza y marcan una característica propia de lo natural.

Como se vio, son importantes porque describen una forma que facilita la circulación de los flujos a través de ellas. La selección natural actúa sobre los sistemas naturales de forma tal que adquieren diseños que propenden a que el intercambio de flujos se pueda llevar a cabo de acuerdo a la ley cosntructal.

Algunas de las propiedades de este tipo de distribuciones ya se han visto en el capítulo mencionado, ahora analizaremos otras que nos servirán como una valiosísima herramienta a la hora trabajar con las comunidades de interacción directa, más específicamente nos posibilitarán comprender cómo opera en ellas la fraternidad.

Para comenzar con nuestro análisis vamos a recurrir a área relativamente nuevo en las matemáticas, los fractales; no para analizar qué son ni para qué sirven, sino como una herramienta de análisis de las estructuras propias de las redes sociales de interacción directas.

Sobre Fractales simplemente diremos que son objetos matemáticos que se pueden descomponer en partes menores semejantes a la primitiva. El término fue propuesto por Benoît Mandelbrot en 1975 y deriva del Latín fractus, que significa quebrado o fracturado. Su descubridor define fractal The Fractal Geometry of Nature (1982) como: "una forma geométrica irregular o fragmentada que puede ser dividida en partes, cada una de las cuales es (al menos aproximadamente) una copia reducida del todo".

Hay fractales por doquier en la naturaleza. Ilustraremos su proceso constructivo con El triángulo de Sierpinski. Partiendo desde un triángulo equilátero dividiendo su altura y su ancho por la mitad se obtienen tres triángulos idénticos, semejantes al original, solo que sus alturas y sus bases son la mitad que las del primitivo.

http://en.wikipedia.org/wiki/File:Animated_construction_of_Sierpinski_Triangle.gif

Lo interesante que pasa con esta figura es ver cómo a partir de la división por dos de su sus lados se obtienen tres triángulos semejantes al original. Más adelante volveremos sobre este triángulo, pero ahora vamos a ver otras figuras más conocidas para nosotros como son la recta, el cuadrado y el cubo a las que someteremos al mismo proceso de fraccionamientos sucesivos

Consideremos una barra de largo L, si duplicamos su longitud tendremos dos copias proporcionales de la barra original. Lo mismo ocurre si partimos el segmento en dos segmentos L/2.

2 segmentos de tamaño 1/2:	N=2, L=1/2	(1/2)-1 = 2	N / (L)-1 = 1
4 segmentos de tamaño 1/4:	N=4, L=1/4	(1/4)-1 = 4	N / (L)-1 = 1
8 segmentos de tamaño 1/8:	N=8, L=1/8	(1/8)-1 = 8	N / (L)-1 = 1
..................	........	..........	..........
2n segmentos de tamaño (1/2)n:	N=2n , L=(1/2n)	L-1 = N	N / (L)-1 = 1

Repitamos el mismo proceso para un cuadrado de lado = L y lo dividimos en cuadrados mas chicos de lado L/2 y L/4

4 cuadrados de tamaño 1/2:	N=4, L=1/2	(1/2)-2 = 4	N / (L)-2 = 1
16 cuadrados de tamaño 1/4:	N=16, L=1/4	(1/4)-2 = 16	N / (L)-2 = 1
64 cuadrados de tamaño 1/8:	N=64, L=1/8	(1/8)-2 = 64	N / (L)-2 = 1
..................	........	..........	..........
22n cuadrados de tamaño 1/2n:	N=22n , L=1/2n	L-2 = N	N / (L)-2 = 1

Por último intentémoslo con el cubo de arista L, que también segmentamos en cubitos de lado L/2 y L/4

8 cubos de arista 1/2:	N=8, L=1/2	(1/2)-3 = 8	N / (L)-3 = 1
64 cubos de arista 1/4:	N=64, L=1/4	(1/4)-3 = 64	N / (L)-3 = 1
512 cubos de arista 1/8:	N=512, L=1/8	(1/8)-3 = 512	N / (L)-3 = 1
...............	...............	...............
23n cubos de arista 1/2n:	N=23n , L=1/2n	L-3 = N	N / (L)-3 = 1

Como vemos en cada caso en la columna de la derecha la relación N / (L)^-D en todos los casos nos da 1 y D es una característica propia para cada objeto gráfico del que se trate.

Estableciendo una relación genérica para estas figuras por todos conocidas vemos que

N= L^-D [ecuación 5]

Siendo N las veces que amplifico el objeto original y L la cantidad de objetos que veo luego de dicha amplificación.

La dimensión D es simplemente el exponente de la ecuación que relaciona el número de partes similares que se obtienen al romper el todo que quedan de manifiesto al ampliar N veces el tamaño original del objeto.

A diferencia de los objetos de la geometría euclidiana, en el mundo de los fractales nos podemos encontrar con dimensiones que nos son números enteros, tal es el caso del triángulo de Sierpinski al que vamos a someter al mismo proceso de análisis como hicimos con las otra figuras. Recordemos que procedíamos partiendo sus lados en mitades (alto y ancho) y que producto de esa partición se obtenían tres triángulos semejantes, siguiendo este proceso llegamos a esta tabla

3 triángulos de lado 1/2:	N=3, L=1/2	(1/2)-D = 3
9 triángulos de lado 1/4:	N=9, L=1/4	(1/4)-D = 9
27 triángulos de lado 1/8:	N=27, L=1/8	(1/8)-D = 27
...............	...............	...............
3n triángulos de lado 1/2n:	N=3n , L=1/2n	(1/2n )-D = 3n

¿Que valor tendrá D para el caso del triángulo de Sierpinski? ¿Cómo encontramos el exponente D en este caso? Despejando D de la ecuación 1 mediante el uso de logaritmos tenemos que:

D = - Log (N)/ log (L)

Lo primero que hacíamos era contra cuantos objetos similares teníamos al amplificar la figura n veces. En este caso N es igual a 3 y L es igual a 1/2

D = - Log (3) / log (1/2) = 1,585

La dimensión del triángulo de Sierpinski es D = 1,585 que en términos de lo conocido sería una dimensión que estaría entre las dimensiones del plano y de la línea.

Generalizando la definición podemos decir que

Dimensión fractal = log (numero de piezas obtenidas)/ log(factor de amplificación) [ecuación 6]

Le ecuación 2 del capítulo tres nos mostraba relación matemática del tipo Ley potencial o más conocida por su nombre en inglés Power Law

f(x) = a x^k

en donde a (la constante de proporcionalidad) y k (el exponente de la potencia) eran constantes. La ley potencial y nuestra definición de dimensión fractal difieren en una constante que es demostrable que tiene que ver con un coeficiente de autosimilitud.

Lo importante ahora es ver que tanto la eq 1 log(fx) = Log a + k Log x = log a x^k y la definición de dimensión fractal son prácticamente idénticas.

Cuando se estudia la ley de alometría, que es una power law que establece un tipo de relación log(fx) = a Log x, se hace referencia a que “a” es un exponente de escala, dado que la ley de alometría trata justamente con los cambios de escala de una muestra estadística. En el caso de la ley de Kleiber, que se veía en ese capítulo, se relacionaba el cambio del volumen en los animales a partir del incremento de su tasa metabólica. En el caso de la ley de Kleiber ese exponente era 3/4. Esto quiere decir que la dimensión fractal de la ley de Kleiber sería de 0,75.

También se puede determinar la dimensión fractal a partir de las relaciones de escala. Este es el método más usado a partir de medidas experimentales. Recordemos aquella vieja técnica para cambiar de escala a un dibujo que usábamos en la escuela. Sobre el dibujo a amplificar se sobreponía una grilla de un tamaño de cuadrados determinado. Sobre una nueva hoja de papel se dibujaba una nueva grilla con un tamaño de cuadrados mayores o menores al original de acuerdo a lo que se quisiere hacer, aumentar o disminuir el dibujo original. Luego se dibujaba sobre la nueva grilla lo que correspondía a ese cuadrado del damero original tratando de hacer lo mejor posible, dentro del cuadrado, la representación del dibujo original que correspondiere.

Lo que hace la ley de potencia es un cambio de escala entre dos escenarios distintos, compensando los defasajes que se producen debido a ese cambio de escala mediante una constante de proporcionalidad asociable a la dimensión de los fractales.

Como señalan Bartolo Luque y Aida Agea en su curso de fractales

“existe todo un repertorio de dimensiones. Conceptualmente cada una determina una propiedad distinta del objeto geométrico sobre el que la medimos. Podemos hacer tres grandes grupos:

1. Dimensión fractal (p.ej. dimensión de autosimilaridad, de capacidad o de Hausdorff): se refieren a como el objeto geométrico llena el espacio en el que está inmerso. Las dimensiones fractales pueden ser enteras o fraccionarias.

2. Dimensión topológica (p.ej.: dimensión de recubrimiento o iterativa): nos hablan de la conectividad de los puntos del objeto de medida. Nos dice si nuestro objeto es una arista, un plano, un volumen, un hipervolumen, etc. Su valor es siempre entero.

3. Dimensión de inmersión (Embedding dimension): se refiere al espacio que contiene al objeto de estudio. Puede ser de nuevo entera o fraccionaria.

Por lo pronto un espacio fraternal encontramos estas tres descripciones

Recordemos la forma de una power law

"Las power laws son las características generales emergentes que presentan los sistemas complejos”

Citado por Peter Winiwarter de The fractal nature of nature: power laws, ecological complexity and biodiversity- James H. Brown, et all en el capítulo mencionado.

“A pesar de la complejidad y de la idiosincrasia de los organismos y ecosistemas en que se producen, hay aspectos en la estructura y en las funciones de estos sistemas que se mantienen auto-similares, o casi, dentro de una amplia gama de escalas espaciales y temporales. Leyes potenciales empíricas describen matemáticamente una jerarquía de tipo fractal en la organización de estos sistemas.” […]“ Por otra parte, mecanismos sencillos que limitan la estructura y la dinámica a mayor escala, también establecen grandes limitaciones sobre cómo los componentes interactúan y se vinculan a gran escala, los sistemas complejo. Juntos, estos mecanismos de abajo para arriba y de arriba para abajo dan lugar a Power Laws y otras características emergentes".

Las power laws son, en consecuencia, lo que mantiene autosimilitud a media que el sistema evoluciona y esto puede interpretarse gráficamente como la evolución que presenta un fractal a medida que se va autogenerando.

El tercer elemento que queríamos introducir referente al tema que nos compete en este capítulo es la jerarquía fractal. Llamaremos jerarquía fractal un ordenamiento emergente propio de la power Law. Si a una power law le corresponde un fractal es evidente que podemos interpretar a las power laws como sistemas evolutivos en el tiempo que por ser fractales se crean de una matriz y evolucionan en un sentido tal que su complejidad aumenta, y a medida que lo hacen, van generando nuevas generaciones emergentes de orden superior a la anterior. Este procedo de desarrollo factal establece una jerarquía.

Determinado un X cualquiera en el eje de ordenadas, a las x que están a la derecha de X le corresponderán f(x) menores (mayores) que a X, en consecuencia a las que se encuentren a su izquierda le corresponderán f(x) mayores (menores). Así se establece un ordenamiento de mayor a menor o de menor a mayor propio de la distribución muestral de la que se trate, la pendiente de la recta de su representación doble logarítmica, nos dará una idea de cuan diferentes son entre sí los sucesivos muestreos y cuan disímil será la distribución como conjunto. A mayor pendiente de la recta doblelogarítmica mayor será la jerarquía fractal entre sus elementos primitivos. Cuanto mayor sea su dimensión fractal mas rápido será el crecimiento de sus partes al aumentar el factor de aumento.

Pero para verlo mejor gráficamente vamos tomar una porción de la curva y la vamos a amplificar en un sector correspondiente al vecindario de X (Δx).

Para cualquier x encontraremos una porción de la curva f(x) tal que en un Δx, f(x) decrece (crece) desde a hasta b. En dicho Δx encontramos un Δy= f(a)- f(x) que tendrá un valor opuesto a otro Δy= f(b)- f(x), representado en la figura por flechas de sentido opuesto.

Esto es fundamental ya que siempre que se pretenda reunir una diversidad social, tal que su dispersión sea Δx, se establecerá una tensión interna que dependerá de la forma propia de la curva y del sector donde se tome el Δx.

La diversidad Δx está sujeta una tensión intrínseca que provoca un desequilibrio propio de la diversidad y que el sistema social en cuestión debe resolver para poder convivir y sostenerse en el tiempo. Esta tensión opuesta y de magnitud relativa al sector de la curva en cuestión, provoca un momento cinético que produce la movilidad social necesaria para que este diferencial pueda evolucionar en un sentido o en otro. Es por eso que ese sistema social lo resuelve, como dice Juán Urrutia Elejalde en el Capitalismo que viene al describir el concepto de Fraternidad, como una conveniencia de los agentes en la búsqueda de un equilibrio dentro de la red: "cada hermano está dispuesto a no ser el más listo para permanecer unido a su hermano." El Δy es el máximo esfuerzo que cada agente está dispuesto a hacer en favor de la cohesión social.

Para que un ser humano (agente de una red de interacción directa) pueda hacer sustentable su vida necesitará reunirse con un grupo social para que en conjunto colaboren en la empresa creadora que es la vida.

Ahora, si bien siempre existen estas tensiones emergentes propias de cualquier agrupamiento social, el agente deberá optar por un Δx con el cual asociarse; dicho de otra forma elegir el sector de la curva que esté en concordancia con lo que mejor le convenga. Porque hay formas distintas de lograr número ya que en una porción de la curva el número se logra a partir de una gran diversidad pero con poca tensión social relativa ( sector derecho) y en el otro se logra con una gran paridad pero con tensiones sociales mucho mayores.

Si el agente opta por agremiarse a la porción derecha de la curva, esto es minorías muy dispares entre sí y con una gran dispersión, las tensiones internas producidas serán mínimas dado que la curva en ese sector está bastante aplanada. Esto es producto del equilibrio numeral entre los diferentes actores que la hace homogénea numeralmente en la diversidad. La escasa tensión social posibilitará el diálogo y el arreglo racional mediante la implementación del contrato social.

Por el contrario si tomamos una muestra de la porción izquierda de la curva, a pequeños Δx tendremos una gran tensión social debido a la pronunciada pendiente de la curva en ese sector. Por lo que el agrupamiento social en este sector, para ser equilibrado deberá se muy poco disperso, contrariamente a lo que pasaba en el caso anterior. Este es el caso del populismo, el consenso se logra en base a la casi nula dispersión, a un alto grado de conflictividad latentes, y a un equilibrio muy inestable que ante cualquier perturbación puede desencadenar la ruptura social. En este caso la comunicación social es encintamente emocional.

Generalizando, los agrupamiento sociales del sector izquierdo de la curva serán mas numerosos y homogéneos aunque menos estables, los del derecho serán menos numerosos mas heterogéneos pero pese a esto mas estables. Podemos representar esto mediante dos rectángulos oblongos de superficies equivalentes que contienen el mismo número de agentes cada uno, en el primer caso el rectángulo se encuentra parado con una pequeña base de sustentación y una gran altura (rectángulo verde), en el segundo caso, el rectángulo yace acostado con su lado mayor como base (rectángulo rojo), es evidente que este segundo rectángulo pese a mostrar una gran diversidad, tiene mas posibilidades que sobrevivir que el primero.

Otra consecuencia de este análisis surge a partir de lo que Luque y Agea definen como Dimensión de inmersión. Conceptuar a los sistemas sociales como sectores estancos (Δx fijos) es un error, porque si bien en general las power laws son discretas y no una línea continua como las dibujadas, los agrupamientos discretos están sujetos a una movilidad ascendente o descendente en la curva. De allí la dimensión inmersa se yergue como una propiedad medible fundamental dentro de las power laws.

Imaginemos un sistema social familiar como el que hemos venido discutiendo en los últimos capítulos, por ejemplo una familia matricial sindiásmica, si bien vemos una separación entre padres e hijos que es evidente, y dentro del grupo de los hermanos también se puede apreciar una cierta distancia social, hay un salto de escala entre generación y generación y también un cambio de escala dentro de una misma generación de hermanos. Pese a esto también hay cierto hilo conductor de similitud entre agente y agente tal que nunca se puede determinar a ciencia cierta el comienzo o el fin de una familia determinada o de toda una gens, sino que hay un devenir continuo dado que los hermanos se convierten en padres y luego en abuelos y así de generación en generación las gens van teniendo un movimiento ascendente en la curva de la power law, aunque permanezcan siendo siempre la misma gens.

Esto se puede interpretar como un continuo de remolinos que se producen en los diferentes estadíos de evolución de la power law, como bucles producidos por los momentos sociales descriptos que avanzan unos sobre los otros incorporándolos y deglutiéndolos de menor a mayor, y a media que lo hacen todo el sistema evoluciona con un movimiento ascendente de conjunto. Dicho esto estamos en condiciones de analizar la curva como una sucesión de rizos o rizomas ascendentes que trepan la pendiente evolutiva del sistema social.

Sobre la dimensión fractal ya hemos hablado al describir la evolución del sistema social en su emergencia desde una generación a otra, mediante la inmersión de uno dentro del otro, solo nos quedaría analizar la dimensión topológica, que tiene que ver con la forma en que la red social está comunicada y de cómo, a partir de esa topología, evolucionan sus flujos. Es por eso que ahora nos centraremos en la conectividad de la red y sus posibilidades.