En este capítulo intentaremos mostrar como se relacionan las redes sociales con las redes de libre escala a través de las distribuciones PZM descriptas en el capítulo 3. Este tipo de distribuciones son muy interesantes debido que se encuentran por doquier en la naturaleza y marcan una característica propia de lo natural.
Como se vio, son importantes porque describen una forma que facilita la circulación de los flujos a través de ellas. La selección natural actúa sobre los sistemas naturales de forma tal que adquieren diseños que propenden a que el intercambio de flujos se pueda llevar a cabo de acuerdo a la ley cosntructal.
Algunas de las propiedades de este tipo de distribuciones ya se han visto en el capítulo mencionado, ahora analizaremos otras que nos servirán como una valiosísima herramienta a la hora trabajar con las comunidades de interacción directa, más específicamente nos posibilitarán comprender cómo opera en ellas la fraternidad.

Para comenzar con nuestro análisis vamos a recurrir a área relativamente nuevo en las matemáticas, los fractales; no para analizar qué son ni para qué sirven, sino como una herramienta de análisis de las estructuras propias de las redes sociales de interacción directas.
Sobre Fractales simplemente diremos que son objetos matemáticos que se pueden descomponer en partes menores semejantes a la primitiva. El término fue propuesto por Benoît Mandelbrot en 1975 y deriva del Latín fractus, que significa quebrado o fracturado. Su descubridor define fractal The Fractal Geometry of Nature (1982) como: "una forma geométrica irregular o fragmentada que puede ser dividida en partes, cada una de las cuales es (al menos aproximadamente) una copia reducida del todo".
Hay fractales por doquier en la naturaleza. Ilustraremos su proceso constructivo con El triángulo de Sierpinski. Partiendo desde un triángulo equilátero dividiendo su altura y su ancho por la mitad se obtienen tres triángulos idénticos, semejantes al original, solo que sus alturas y sus bases son la mitad que las del primitivo.

http://en.wikipedia.org/wiki/File:Animated_construction_of_Sierpinski_Triangle.gif
Lo interesante que pasa con esta figura es ver cómo a partir de la división por dos de su sus lados se obtienen tres triángulos semejantes al original. Más adelante volveremos sobre este triángulo, pero ahora vamos a ver otras figuras más conocidas para nosotros como son la recta, el cuadrado y el cubo a las que someteremos al mismo proceso de fraccionamientos sucesivos
Consideremos una barra de largo L, si duplicamos su longitud tendremos dos copias proporcionales de la barra original. Lo mismo ocurre si partimos el segmento en dos segmentos L/2.
| 2 segmentos de tamaño 1/2: | N=2, L=1/2 | (1/2)-1 = 2 | N / (L)-1 = 1 |
| 4 segmentos de tamaño 1/4: | N=4, L=1/4 | (1/4)-1 = 4 | N / (L)-1 = 1 |
| 8 segmentos de tamaño 1/8: | N=8, L=1/8 | (1/8)-1 = 8 | N / (L)-1 = 1 |
| .................. | ........ | .......... | .......... |
| 2n segmentos de tamaño (1/2)n: | N=2n , L=(1/2n) | L-1 = N | N / (L)-1 = 1 |
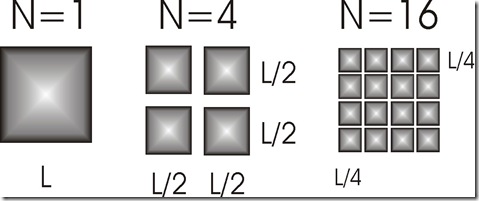
Repitamos el mismo proceso para un cuadrado de lado = L y lo dividimos en cuadrados mas chicos de lado L/2 y L/4
| 4 cuadrados de tamaño 1/2: | N=4, L=1/2 | (1/2)-2 = 4 | N / (L)-2 = 1 |
| 16 cuadrados de tamaño 1/4: | N=16, L=1/4 | (1/4)-2 = 16 | N / (L)-2 = 1 |
| 64 cuadrados de tamaño 1/8: | N=64, L=1/8 | (1/8)-2 = 64 | N / (L)-2 = 1 |
| .................. | ........ | .......... | .......... |
| 22n cuadrados de tamaño 1/2n: | N=22n , L=1/2n | L-2 = N | N / (L)-2 = 1 |
Por último intentémoslo con el cubo de arista L, que también segmentamos en cubitos de lado L/2 y L/4
| 8 cubos de arista 1/2: | N=8, L=1/2 | (1/2)-3 = 8 | N / (L)-3 = 1 |
| 64 cubos de arista 1/4: | N=64, L=1/4 | (1/4)-3 = 64 | N / (L)-3 = 1 |
| 512 cubos de arista 1/8: | N=512, L=1/8 | (1/8)-3 = 512 | N / (L)-3 = 1 |
| ............... | ............... | ............... |
|
| 23n cubos de arista 1/2n: | N=23n , L=1/2n | L-3 = N | N / (L)-3 = 1 |
Como vemos en cada caso en la columna de la derecha la relación N / (L)-D en todos los casos nos da 1 y D es una característica propia para cada objeto gráfico del que se trate.
Estableciendo una relación genérica para estas figuras por todos conocidas vemos que
N= L-D [ecuación 5]
Siendo N las veces que amplifico el objeto original y L la cantidad de objetos que veo luego de dicha amplificación.
La dimensión D es simplemente el exponente de la ecuación que relaciona el número de partes similares que se obtienen al romper el todo que quedan de manifiesto al ampliar N veces el tamaño original del objeto.
A diferencia de los objetos de la geometría euclidiana, en el mundo de los fractales nos podemos encontrar con dimensiones que nos son números enteros, tal es el caso del triángulo de Sierpinski al que vamos a someter al mismo proceso de análisis como hicimos con las otra figuras. Recordemos que procedíamos partiendo sus lados en mitades (alto y ancho) y que producto de esa partición se obtenían tres triángulos semejantes, siguiendo este proceso llegamos a esta tabla
| 3 triángulos de lado 1/2: | N=3, L=1/2 | (1/2)-D = 3 |
| 9 triángulos de lado 1/4: | N=9, L=1/4 | (1/4)-D = 9 |
| 27 triángulos de lado 1/8: | N=27, L=1/8 | (1/8)-D = 27 |
| ............... | ............... | ............... |
| 3n triángulos de lado 1/2n: | N=3n , L=1/2n | (1/2n )-D = 3n |
¿Que valor tendrá D para el caso del triángulo de Sierpinski? ¿Cómo encontramos el exponente D en este caso? Despejando D de la ecuación 1 mediante el uso de logaritmos tenemos que:
D = - Log (N)/ log (L)
Lo primero que hacíamos era contra cuantos objetos similares teníamos al amplificar la figura n veces. En este caso N es igual a 3 y L es igual a 1/2
D = - Log (3) / log (1/2) = 1,585
La dimensión del triángulo de Sierpinski es D = 1,585 que en términos de lo conocido sería una dimensión que estaría entre las dimensiones del plano y de la línea.
Generalizando la definición podemos decir que
Dimensión fractal = log (numero de piezas obtenidas)/ log(factor de amplificación) [ecuación 6]
Le ecuación 2 del capítulo tres nos mostraba relación matemática del tipo Ley potencial o más conocida por su nombre en inglés Power Law
f(x) = a xk
en donde a (la constante de proporcionalidad) y k (el exponente de la potencia) eran constantes. La ley potencial y nuestra definición de dimensión fractal difieren en una constante que es demostrable que tiene que ver con un coeficiente de autosimilitud.
Lo importante ahora es ver que tanto la eq 1 log(fx) = Log a + k Log x = log a xk y la definición de dimensión fractal son prácticamente idénticas.
Cuando se estudia la ley de alometría, que es una power law que establece un tipo de relación log(fx) = a Log x, se hace referencia a que “a” es un exponente de escala, dado que la ley de alometría trata justamente con los cambios de escala de una muestra estadística. En el caso de la ley de Kleiber, que se veía en ese capítulo, se relacionaba el cambio del volumen en los animales a partir del incremento de su tasa metabólica. En el caso de la ley de Kleiber ese exponente era 3/4. Esto quiere decir que la dimensión fractal de la ley de Kleiber sería de 0,75.
También se puede determinar la dimensión fractal a partir de las relaciones de escala. Este es el método más usado a partir de medidas experimentales. Recordemos aquella vieja técnica para cambiar de escala a un dibujo que usábamos en la escuela. Sobre el dibujo a amplificar se sobreponía una grilla de un tamaño de cuadrados determinado. Sobre una nueva hoja de papel se dibujaba una nueva grilla con un tamaño de cuadrados mayores o menores al original de acuerdo a lo que se quisiere hacer, aumentar o disminuir el dibujo original. Luego se dibujaba sobre la nueva grilla lo que correspondía a ese cuadrado del damero original tratando de hacer lo mejor posible, dentro del cuadrado, la representación del dibujo original que correspondiere.
Lo que hace la ley de potencia es un cambio de escala entre dos escenarios distintos, compensando los defasajes que se producen debido a ese cambio de escala mediante una constante de proporcionalidad asociable a la dimensión de los fractales.
Como señalan Bartolo Luque y Aida Agea en su curso de fractales
“existe todo un repertorio de dimensiones. Conceptualmente cada una determina una propiedad distinta del objeto geométrico sobre el que la medimos. Podemos hacer tres grandes grupos:
1. Dimensión fractal (p.ej. dimensión de autosimilaridad, de capacidad o de Hausdorff): se refieren a como el objeto geométrico llena el espacio en el que está inmerso. Las dimensiones fractales pueden ser enteras o fraccionarias.
2. Dimensión topológica (p.ej.: dimensión de recubrimiento o iterativa): nos hablan de la conectividad de los puntos del objeto de medida. Nos dice si nuestro objeto es una arista, un plano, un volumen, un hipervolumen, etc. Su valor es siempre entero.
3. Dimensión de inmersión (Embedding dimension): se refiere al espacio que contiene al objeto de estudio. Puede ser de nuevo entera o fraccionaria.
Por lo pronto un espacio fraternal encontramos estas tres descripciones
Recordemos la forma de una power law
"Las power laws son las características generales emergentes que presentan los sistemas complejos”
Citado por Peter Winiwarter de The fractal nature of nature: power laws, ecological complexity and biodiversity- James H. Brown, et all en el capítulo mencionado.
“A pesar de la complejidad y de la idiosincrasia de los organismos y ecosistemas en que se producen, hay aspectos en la estructura y en las funciones de estos sistemas que se mantienen auto-similares, o casi, dentro de una amplia gama de escalas espaciales y temporales. Leyes potenciales empíricas describen matemáticamente una jerarquía de tipo fractal en la organización de estos sistemas.” […]“ Por otra parte, mecanismos sencillos que limitan la estructura y la dinámica a mayor escala, también establecen grandes limitaciones sobre cómo los componentes interactúan y se vinculan a gran escala, los sistemas complejo. Juntos, estos mecanismos de abajo para arriba y de arriba para abajo dan lugar a Power Laws y otras características emergentes".
Las power laws son, en consecuencia, lo que mantiene autosimilitud a media que el sistema evoluciona y esto puede interpretarse gráficamente como la evolución que presenta un fractal a medida que se va autogenerando.
El tercer elemento que queríamos introducir referente al tema que nos compete en este capítulo es la jerarquía fractal. Llamaremos jerarquía fractal un ordenamiento emergente propio de la power Law. Si a una power law le corresponde un fractal es evidente que podemos interpretar a las power laws como sistemas evolutivos en el tiempo que por ser fractales se crean de una matriz y evolucionan en un sentido tal que su complejidad aumenta, y a medida que lo hacen, van generando nuevas generaciones emergentes de orden superior a la anterior. Este procedo de desarrollo factal establece una jerarquía.
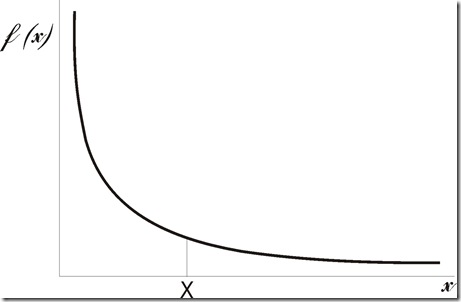
Determinado un X cualquiera en el eje de ordenadas, a las x que están a la derecha de X le corresponderán f(x) menores (mayores) que a X, en consecuencia a las que se encuentren a su izquierda le corresponderán f(x) mayores (menores). Así se establece un ordenamiento de mayor a menor o de menor a mayor propio de la distribución muestral de la que se trate, la pendiente de la recta de su representación doble logarítmica, nos dará una idea de cuan diferentes son entre sí los sucesivos muestreos y cuan disímil será la distribución como conjunto. A mayor pendiente de la recta doblelogarítmica mayor será la jerarquía fractal entre sus elementos primitivos. Cuanto mayor sea su dimensión fractal mas rápido será el crecimiento de sus partes al aumentar el factor de aumento.
Pero para verlo mejor gráficamente vamos tomar una porción de la curva y la vamos a amplificar en un sector correspondiente al vecindario de X (Δx).
Para cualquier x encontraremos una porción de la curva f(x) tal que en un Δx, f(x) decrece (crece) desde a hasta b. En dicho Δx encontramos un Δy= f(a)- f(x) que tendrá un valor opuesto a otro Δy= f(b)- f(x), representado en la figura por flechas de sentido opuesto.
Esto es fundamental ya que siempre que se pretenda reunir una diversidad social, tal que su dispersión sea Δx, se establecerá una tensión interna que dependerá de la forma propia de la curva y del sector donde se tome el Δx.
La diversidad Δx está sujeta una tensión intrínseca que provoca un desequilibrio propio de la diversidad y que el sistema social en cuestión debe resolver para poder convivir y sostenerse en el tiempo. Esta tensión opuesta y de magnitud relativa al sector de la curva en cuestión, provoca un momento cinético que produce la movilidad social necesaria para que este diferencial pueda evolucionar en un sentido o en otro. Es por eso que ese sistema social lo resuelve, como dice Juán Urrutia Elejalde en el Capitalismo que viene al describir el concepto de Fraternidad, como una conveniencia de los agentes en la búsqueda de un equilibrio dentro de la red: "cada hermano está dispuesto a no ser el más listo para permanecer unido a su hermano." El Δy es el máximo esfuerzo que cada agente está dispuesto a hacer en favor de la cohesión social.
Para que un ser humano (agente de una red de interacción directa) pueda hacer sustentable su vida necesitará reunirse con un grupo social para que en conjunto colaboren en la empresa creadora que es la vida.
Ahora, si bien siempre existen estas tensiones emergentes propias de cualquier agrupamiento social, el agente deberá optar por un Δx con el cual asociarse; dicho de otra forma elegir el sector de la curva que esté en concordancia con lo que mejor le convenga. Porque hay formas distintas de lograr número ya que en una porción de la curva el número se logra a partir de una gran diversidad pero con poca tensión social relativa ( sector derecho) y en el otro se logra con una gran paridad pero con tensiones sociales mucho mayores.
Si el agente opta por agremiarse a la porción derecha de la curva, esto es minorías muy dispares entre sí y con una gran dispersión, las tensiones internas producidas serán mínimas dado que la curva en ese sector está bastante aplanada. Esto es producto del equilibrio numeral entre los diferentes actores que la hace homogénea numeralmente en la diversidad. La escasa tensión social posibilitará el diálogo y el arreglo racional mediante la implementación del contrato social.
Por el contrario si tomamos una muestra de la porción izquierda de la curva, a pequeños Δx tendremos una gran tensión social debido a la pronunciada pendiente de la curva en ese sector. Por lo que el agrupamiento social en este sector, para ser equilibrado deberá se muy poco disperso, contrariamente a lo que pasaba en el caso anterior. Este es el caso del populismo, el consenso se logra en base a la casi nula dispersión, a un alto grado de conflictividad latentes, y a un equilibrio muy inestable que ante cualquier perturbación puede desencadenar la ruptura social. En este caso la comunicación social es encintamente emocional.
Generalizando, los agrupamiento sociales del sector izquierdo de la curva serán mas numerosos y homogéneos aunque menos estables, los del derecho serán menos numerosos mas heterogéneos pero pese a esto mas estables. Podemos representar esto mediante dos rectángulos oblongos de superficies equivalentes que contienen el mismo número de agentes cada uno, en el primer caso el rectángulo se encuentra parado con una pequeña base de sustentación y una gran altura (rectángulo verde), en el segundo caso, el rectángulo yace acostado con su lado mayor como base (rectángulo rojo), es evidente que este segundo rectángulo pese a mostrar una gran diversidad, tiene mas posibilidades que sobrevivir que el primero.
Otra consecuencia de este análisis surge a partir de lo que Luque y Agea definen como Dimensión de inmersión. Conceptuar a los sistemas sociales como sectores estancos (Δx fijos) es un error, porque si bien en general las power laws son discretas y no una línea continua como las dibujadas, los agrupamientos discretos están sujetos a una movilidad ascendente o descendente en la curva. De allí la dimensión inmersa se yergue como una propiedad medible fundamental dentro de las power laws.
Imaginemos un sistema social familiar como el que hemos venido discutiendo en los últimos capítulos, por ejemplo una familia matricial sindiásmica, si bien vemos una separación entre padres e hijos que es evidente, y dentro del grupo de los hermanos también se puede apreciar una cierta distancia social, hay un salto de escala entre generación y generación y también un cambio de escala dentro de una misma generación de hermanos. Pese a esto también hay cierto hilo conductor de similitud entre agente y agente tal que nunca se puede determinar a ciencia cierta el comienzo o el fin de una familia determinada o de toda una gens, sino que hay un devenir continuo dado que los hermanos se convierten en padres y luego en abuelos y así de generación en generación las gens van teniendo un movimiento ascendente en la curva de la power law, aunque permanezcan siendo siempre la misma gens.
Esto se puede interpretar como un continuo de remolinos que se producen en los diferentes estadíos de evolución de la power law, como bucles producidos por los momentos sociales descriptos que avanzan unos sobre los otros incorporándolos y deglutiéndolos de menor a mayor, y a media que lo hacen todo el sistema evoluciona con un movimiento ascendente de conjunto. Dicho esto estamos en condiciones de analizar la curva como una sucesión de rizos o rizomas ascendentes que trepan la pendiente evolutiva del sistema social.
Sobre la dimensión fractal ya hemos hablado al describir la evolución del sistema social en su emergencia desde una generación a otra, mediante la inmersión de uno dentro del otro, solo nos quedaría analizar la dimensión topológica, que tiene que ver con la forma en que la red social está comunicada y de cómo, a partir de esa topología, evolucionan sus flujos. Es por eso que ahora nos centraremos en la conectividad de la red y sus posibilidades.






















































4 nos acompañaron:
Hola. Los agrupamientos sociales del sector izquierdo, ¿Se asemejarían al bipartidismo de los países "serios" ?. Saludos.
Mermelada, debo ser absolutamente sincero, un ha habido capítulo que me costó mas que este y no está terminado. Por si no se entendió, la derecha de la curva se podría asociar a lo que se conoce por “pertenencia de clase”. Si bien hay deferencias marcada por posturas contradictorias, la pertenencia a ese sector de la curva, la derecha, hace posible un corpus debido a la escasa diferencia cuantitativa entre sectores. Todas las posturas son minoritaria, por eso no importa cuan distinta sean entre ellas, siempre habrá un “diálogo” posible entre estos sectores. El contrato siempre será posible.
Sobre la izquierda del gráfico se amontonan las posturas mas populares, donde una pequeña dispersión en la diversidad, no solo que agranda el número considerablemente sino que amplia las diferencias, el rectángulo vertical.
Por lo que el modelo no sería el europeo justamente de izquierda y derecha tradicionales, sino la latinoamericana, entre populismo y clases ilustradas contractuales.
Le prometo, le juro, le aseguro, que en la segunda parte de este capítulo voy a ahondar sobre el tema. En realidad es medular que todo este quede claro. en realidad de lo que se trata es de proponer un modelo alternativo a aquel que Ud. menciona, uno mas al uso nostro, lejos, muy lejos de los bi, tri, o multi.
Gracias por pasar
Gracias por la respuesta, muy interesante, siempre con cosas nuevas usted.
Hasta el próximo capítulo, saludos.
Charlie, te citan por acá....
http://www.nacionalypopular.com/index.php?option=com_content&task=view&id=12271&Itemid=208
Saludos!
Publicar un comentario