Nota: Para los que vienen siguiendo el desarrollo del Libro "El Siglo de la Fraternidad" 1, 2a, 2b, y 3a como ada e ido, Augusto, Juán y otros, les digo que no teman a la matemática y traten de seguir este post, al final creo que hay algo interesante.
Desde ya gracias seguirnos
Ley constructal
Mi paso por la facultad de ingeniería estuvo marcado por la lógica de la dictadura militar.
En esos tiempos de sangre y plomo existían exámenes de ingreso y había cupos en las universidades del estado Argentino. También había limitaciones de circulación, agremiación y por supuesto de expresión. En el caso de la Universidad Tecnológica Nacional, el formato por el que los militares optado paralos planes de estudio de las carreras de ingeniería no escapaba a esta lógica de restricciones y esquematizaciones y lo resolvieron de la siguiente manera: dos años de ciencias básicas, un años de ciencias básicas de la ingeniería y tres años de especialización.
Por eso de los cupos comencé a cursar ingeniería en la especialidad “química”, que trata esencialmente sobre la termodinámica de los diferentes procesos en donde se intercambia energía en forma de calor. Lo de “química” viene porque en las reacciones que dan lugar a estos procesos producen cambios químicos en la materia. Un buen ingeniero químico, en consecuencia, se debía, y se debe centrar en el estudio de los procesos termodinámica de los sistemas. Es también desde esa lógica que no puede haber un buen ingeniero químico que no sepa termodinámica, la termodinámica era, y lo sigue siendo, el core de la ingeniería química. Para nosotros las leyes de la termodinámica se trasformaron con el tiempo en una religión, fe que en mundo real solo podían profesar los ingenieros, ya que todos los otros se ocupaban de otras cosas.
En la búsqueda de un soporte que explicara lo común en la gran diversidad de distribuciones que responden a las diferentes Power Laws PZM, tan frecuentes en la naturaleza, y como bien solicitara Winiwarter, es que llegamos a una novel teoría sobre procesos mecánicos en donde intervienen flujos, llamada: Teoría Constructal, desarrollada por el ingeniero rumano-americano Adrian Bejan.
Hasta Bejan la termodinámica clásica había obviado preocuparse por las formas o por las estructuras en donde se llevaban a cabo esas transformaciones. Que se cumplieran las leyes era suficiente para el estudio bárbaro de la ingeniería termodinámica, era de esta forma que también cumplíamos con las cuestiones de fe. A partir de la post modernidad, parecería que esa ingeniería tosca se hubiere convertido en una ingeniería “fashion”, en donde el diseño ahora importa. Este punto desde siempre trajo mutuas bromas entre arquitectos e ingenieros. Los primeros se quejaban de los segundos de no respetar ni siquiera las mas mínimas de las normas de diseño y del arte, los segundo caricaturizaban a los primeros con el clásico chiste de que si tuviesen que diseñar una represa hídrica, la harían pero dejando ventanas en sus paredes para que quede mas bonita. De hecho la carrera de diseño industrial estuvo prohibida durante la dictadura y hoy es una carrera con una gran matricula, incluso mucho mayor que la de muchas ramas de la ingeniería.
Cuando la discusión entre arquitectos e ingenieros sobre el diseño aplicado a los productos y procesos típicos de la ingeniería parecía insalvable, aparece Adrián Bejan con su teoría constructal tratando de mediar en el conflicto.
Por las dudas Bejan toma sus recaudos para no herir susceptibilidades cuando dice:
“Es importante reconocer que la ley constructal es diferente a (es decir, complementaria a) las demás leyes de la termodinámica. La ley constructal fue propuesta como adicional a las leyes de la termodinámica.[…]La primera ley establece que la energía del sistema permanece constante. La segunda ley da cuenta que: para las observaciones que se describen como una tendencia en el tiempo, cuando los cambios que se producen en el interior de los sistemas, todos los flujos actúan de una misma y única manera, de mayor a menor. Analíticamente, esta tendencia denota que la entropía del sistema aumenta durante cada cambio.”
“La primera y segunda ley hablan de una caja negro, sin geometría. No dicen nada acerca de las configuraciones (los dibujos, los mapas, las rutas) de las cosas que fluyen.”[…]“La generación de la configuración del flujo es un fenómeno totalmente diferente de la física, que no está representado ni por la primera ni por la segunda ley. La secuencia temporal de los dibujos que el sistema de flujo exhibe a medida que evoluciona, es el fenómeno cubierto por la ley constructal.”
Esta es su definición:
“El fenómeno nuevo es de cómo cada cosa adquiere arquitectura en la dirección del tiempo: las configuraciones existentes sobreviven cuando su cambio en el tiempo se hace hacia configuraciones de flujo más fácil (la ley constructal).”
“La ley constructal también establece que si el sistema cambia su morfología libremente, entonces va a evolucionar, (por ejemplo, como una secuencia constante de estados), tal que su configuración se desarrolle y que sus corrientes fluyan más y más fácilmente. ¿Qué cambia en las propiedades y en los flujos del sistema de una configuración a otra? Depende de lo que está fijo, por ejemplo: lo que impulsa los flujos a través del sistema. En cualquier caso, fluir más y más fácil quiere decir que a nivel global la configuración del sistema posee cada vez menos y menos resistencia, y que la tasa de generación de entropía tiende en una sola dirección: hacia abajo o arriba, dependiendo de qué tipo de forzamiento se fija"
"Todos los ejemplos, desde la alometría los animales a leyes de escala geofísicas, obedecen a lo conocidos y aceptados principios de la física. El hecho de que todos ellos exhiban "desdideño" es el "algo más", que no está cubierto por los conocidos y aceptados principios."
El tamaño de las ciudades y todas las distribuciones PZM se originan en la evolución de un diseño multiescala de los sistemas de flujo que conectan un punto con un área o un punto con un volumen, por lo que si tenemos una distribución de Zipf de el uso de palabras en una lengua debe tener que ver con el modo en que la información fluye entre un punto y un área o un punto y un volumen y en esto tiene que ver la otra distribución de este tipo, la de Dunbar, donde los flujos de información provenientes del neocortex del cerebro se dirigen hacia la comunidad. La información, ya sea por impulsos electroquímicos, como por el habla es el flujo en cuestión que deberá evolucionar hacia formas mas permeable para que ese flujo de información se haga mas fluido y que las formas de la comunicación de la información adquieran cada vez menos y menos resistencia a su paso.
Vale la pena detenerse en esto por un momento, Bejan establece básicamente dos entidades: un punto y un volumen o superficie, uno fijo o moviendose relativamente al otro, el fluido debe viajar en un sentido y si el volumen o la superficie que debe atravesar es lo suficientemente versátil como para que permita su deformación en el tiempo, la evolución de la forma de este volumen (superficie) será en el sentido que facilite al fluido fluir con mayor facilidad. Hay que aclarar que esta ley se cumple no solo para los procesos termodinámicos sino para todos los procesos en donde intervenga un cuerpo (superficie) y un flujo que lo atraviese.
Las redes, en este sentido, pueden representar los volúmenes o las superficies en cuestión y pueden actuar de dos maneras. Como punto hacia el exterior, cuando intercambia materia y energía con el medio y hacia adentro de la red cuando un nodo emite un mensaje y lo quiere propalar a toda la red. En este último caso la circulación del flujo es interno a la red.
--------------------
Hacer ya un tiempo recurrimos a nuestra amiga, la Dra. en matemáticas María Alejandra Rodriguez Hertz, para tratar de que nos hable sobre los procesos ergódicos. Jana es una especialista en el tema y ha puesto a disposición del público lego una esclarecedora página web en donde describe este proceso para el consumo del público masivo que se puede consultar acá: ttp://www.corodebabel.com.ar/Sistemas-Dinamicos-Caoticos/ergodicidad-sistemas-dinamicos-y-otras-yerbas-primera-parte.html
La ergodicidad trata sobre la capacidad que tienen los fluidos de ocupar todo un volumen. Generalizado: si se proyecta un fluido al seno de un líquido (un volumen, una superficie), este se dispersará en todas las direcciones hasta llegar a ocupar el volumen (superficie) completo, si esto ocurre decimos que el proceso es ergódico. En una red un proceso ergódico sería aquel que permita que la información llegue a todos sus componentes con la misma probabilidad.
En su trabajo Jana da un primer ejemplo en donde utiliza la preparación de un “Negroni ergódico sin hielo” para ilustrar el proceso de difusión del Campari en el seno del Gin y del Martini y de cómo actúa para que: "Al cabo de un período suficientemente largo de tiempo, la mayoría de las partículas se pueden encontrar en cualquier parte del espacio de fases con igual probabilidad". De esta forma Boltzmann formula su famosa Hipótesis Ergódica (HE)
En una red un sistema ergódico sería aquel que permite que la información circule por o a través todos los nodos, de toda la red; aquel donde el rastro que va dejando la información, a medida que circula, mancha a todos y cada unos de los nodos con igual probabilidad.
Sin embargo Jana no nos habla de la forma que adquiere el Campari a medida que se va diluyendo en el seno del trago, de hecho en el video que presenta, la inyección del líquido oscuro, que se va introduciendo dentro del vaso de a pequeños golpecitos de jeringa, adquiere formas de hermosos fractales. Pero claro a ni a ella ni a Boltzmann, parece importarles eso, ellos están preocupados con que el líquido ciertamente llegue a todo el volumen. Pero para Adrián Bejan esto no da cuenta de lo mismo
-------------
Entre los ejemplos de distribuciones PZM que dábamos mas arriba (parte 1), citábamos a ley de Kleiber que establece la relación que hay entre el ritmo metabólico q0 y la masa corporal M elevada a la potencia 3/4 para cualquier animal, incluidos los pequeños organismos. De esta ley se desprende la alometría que establece las posibilidades de crecer que tienen los cuerpos vivos sin que el crecimiento afecte su metabolismo. A este fenómeno hacíamos referencia nosotros en el capítulo De hormigueros, bandadas, metrónomos y los problemas de una Reina Roja - Segunda parte, cuando veíamos las estrategias evolutivas de las diferentes especies y de cómo los conglomerados, que teniendo que actuar en conjunto, evolucionaban alternativas creativas para poder sobrellevar este problema. La alometría es el estudio de la relación entre forma y tamaño.
Tanto en el trabajo citado más arriba (parte 1) como en este otro, James H. Brown, Geoffrey B.West, Brian Enquist, y otros científicos entre los que se encuentran matemáticos, físico y por supuesto biólogos, establecen una ley de escala, o de escalamiento entre los seres vivos basados en Kleiber. Es en este paper: A General Model for the Origin of Allometric Scaling Laws in Biology, los científicos generalizan la idea del escalamiento alométrico de los seres vivos (incluidos los mamíferos) de acuerdo a la siguiente premisa: Los seres vivo se sostienen mediante el transporte de materiales a través de una red lineal que se ramifica para distribuirlos a todas las partes del organismo.
Los investigadores construyeron su modelo en base a tres premisas:
- Que se necesita un patrón de tipo fractal ramificado, capaz de llenar el espacio para suministrar los fluidos que sustentan la vida a todas las partes del organismo,
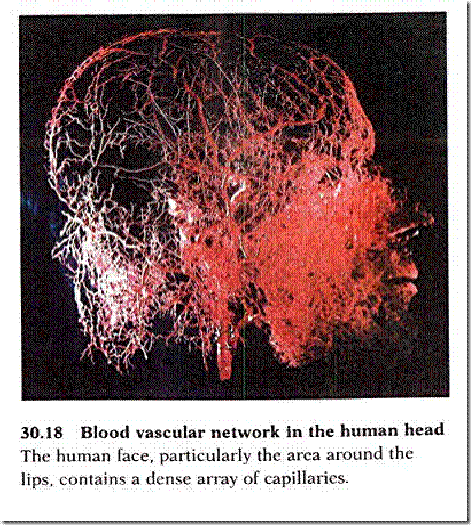
- que la rama final de la red – las nervaduras de los árboles o los capilares del sistema circulatorio – son del mismo tamaño, no importa el tamaño de la “masa corporal” de la especie de la que se trate,
- y que la energía usada para trasportar los recursos a través del la red tiende a ser minimizada.
Es muy interesante esta enuncianción ya que se asemeja mucho a la Ley constructal que establecía “las configuraciones existentes sobreviven cuando su cambio en el tiempo se hace hacia configuraciones de flujo más fácil (la ley constructal).” O la definición que aparece en Wikipedia que es mas fácil de entender:
Para que un sistema de tamaño finito persista en el tiempo (sobreviva), debe desarrollarse de tal manera que facilite el acceso a las corrientes que lo atraviesan.
La facilidad que representa la definición de Bejan es que es mucho mas general y que no hace la distinción de cómo tienen que ser las punteras del sistema. De todas formas el concepto del fractal conductor que distribuye en todo el espacio (volumen-superficie) es magnífico ya que explica el porqué del sistema circulatorio, del sistema respiratorio y muchos procesos naturales se configuran de este modo.
¿Podríamos conceptuar una red social distribuida de esta manera? De tal forma que un miembro de la red pueda hacer circular un mensaje que llegue a TODA la red cumpliendo la hipótesis ergódica expuesta mas arriba. Para verlo mejor vamos a construir un fractal de este tipo en base al modelo que propone acá:
An Escheresque fractal by Peter Raedschelders
- un largo t ( el largo del tronco)
- un ángulo theta θ ( el ángulo que forman las ramas con el tronco).
- una razón r (por la que se establece el largo de la rama en base a una proporción con el tronco.
Se empieza por un segmento (el tronco) de largo t (t>0) que se lo considera como vertical. (Usualmente, consideramos un árbol canónico con un tronco de largo 1.) En la base del tronco está la raíz, en la parte superior fijamos dos ramas, ámbas de largo tr (de largo t o menor que t y mayor que 0).
Cada una de las ramas “forma un ángulo theta θ con la prolongación del tronco”. En el extremo libre de cada una de estas ramas fijamos dos nuevas ramas de largo tr2, nuevamente, formando un ángulo theta θ con la extensión lineal de la rama previa. Continuamos de este modo, adicionando a la nava posición, 2n ramas de largo trn.Algunas notaciones.
En un árbol binario, el único trayecto desde la raíz a cualquier nodo (final de una rama) se puede enunciar especificando una secuencia de derecha (D) o izquierda (I) en cada caso. Por lo tanto una secuencia tal como DID ni solo localiza el nodo en el árbol, también describe el único trayecto desde la raíz al nodo. Las punteras se señalan mediante el signo infinito ∞, como infinitas secuencias de “D” o de “I” y se denotan así “D∞” o de “I∞”Winiwarter muestra unos ejemplos maravillosos de volúmenes y superficies ocupadas por este tipo de árboles fractales:
-----------------------
Ahora hagamos un último ejercicio, consideremos a una red constituida por un árbol fractal binario cuya construcción estuvimos viendo mas arriba. Consideremos que la red es un conglomerado como los del capítulo 2 y que uno de los agentes de la red recibe o percibe algo que debe comunicar a la totalidad de su conglomerado. Digamos que debe avisar de un peligro y que hay que salir disparando.
Hagamos que la red cumpla con lo que postulaba Strogartz:
- Todos los individuos están pendientes de lo que hacen sus vecinos más cercanos.
- Todos los individuos tienen una tendencia a alinearse.
- Todos se acercan a los otros pero manteniendo un distancia mínima entre pares.
- En caso de peligro, salir huyendo.
Lo que le solicitamos a nuestra red de N agentes es que ponga en funcionamiento el punto 4. Para eso el agente que percibe el peligro primero (consideramos que hay un único agente que percibe el estímulo primero) lo debe comunicar con la mayor velocidad y eficiencia a la totalidad del la red. La condición ergódica es elemental, ya que cualquiera de los que no sea avisado es posible que sea arrasado por el riesgo en cuestión.
Para ello se establece como regla de morada una muy simple: tomando en cuenta la dirección de avance del conglomerado el agente Yo, el agente Ego, situado el tope del tronco emite dos mensajes, uno para el agente que está mas cerca suyo a la derecha y otro para el que tiene mas cerca a su izquierda. De esta forma comienza la construcción de un árbol fractal con origen en él mismo. Los agentes D y L reciben el mensaje y tomando como perspectiva de quién viene, realizan la misma operación repitiendo el procedimiento utilizado por Ego, al repetírselo a DD, DI, ID y a II, y así sucesivamente hasta llegar a los nodos punteras. Fin de los mensajes. Todos los nodos procesan la información y actúan en consecuencia.
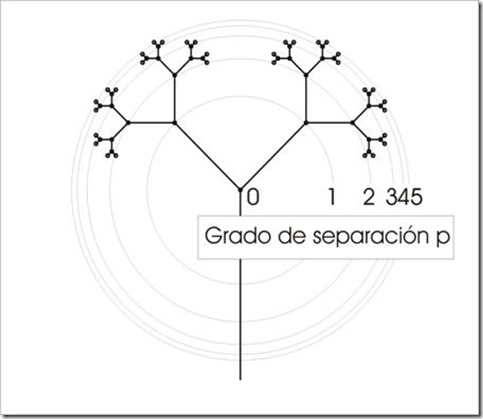
Analicemos el caso del dibujo y trabajemos un poco con los números:
Cantidad de nodos
N= 1+ 2 + 4 + 8 + 16 + 32 = 20 + 21 + 22 + 23 + 24 + 25 = 63
generalizando
N= Σ 2p con n que va desde 0 a p, siendo p el número de saltos o grados de separación, que hay para llegar a las punteras , lo que es lo mismo que decir
Actualizació: Había un error en el nombre de la constante C
N= Σ2p+1 – 1 con n que va desde 1 a p
Cantidad de enlaces C = 2 + 4 + 8 + 16 + 32 = 21 + 22 + 23 + 24 + 25 = 62
generalizando
C= Σ 2p con n que va desde 1 a p, lo que es lo mismo que decir
C= Σ2p+1 – 2
Relación entre ambos
N = C +1
| Grado | 2 a la n | Cant de nodos | Cant de enlaces reales | Cant de enlaces max | Cant de enlaces min | Observaciones |
| 0 | 1,00 | 1 | 0 | 0 | 0 |
|
| 1 | 2,00 | 3 | 2 | 3 | 2 |
|
| 2 | 4,00 | 7 | 6 | 21 | 6 |
|
| 3 | 8,00 | 15 | 14 | 105 | 14 |
|
| 4 | 16,00 | 31 | 30 | 465 | 30 |
|
| 4,69 | 25,81 | 51 | 50 | 1.256 | 50 | Erdos number Red e matemáticos |
| 5 | 32,00 | 63 | 62 | 1.953 | 62 | Karinthy - 1929 |
| 5,5 | 45,25 | 90 | 89 | 3.961 | 89 | Milgram -1967 |
| 6 | 64,00 | 127 | 126 | 8.001 | 126 |
|
| 6,21725 | 74,40 | 148 | 147 | 10.849 | 147 | Número de Dunbar – N = 147,8 |
| 6,5 | 90,51 | 180 | 179 | 16.113 | 179 | Milgran promedio |
| 6,6 | 97,01 | 193 | 192 | 18.530 | 192 | Microsoft - 2007 |
| 6,7 | 103,97 | 207 | 206 | 21.308 | 206 | Watts -Strogartz 2003 |
| 7 | 128,00 | 255 | 254 | 32.385 | 254 |
|
| 8 | 256,00 | 511 | 510 | 130.305 | 510 |
|
| 9 | 512,00 | 1.023 | 1.022 | 522.753 | 1.022 |
|
Lo mas sorprendente de nuestro descubrimiento es que cuando en la progresión que hicimos en la planilla de cálculo, al poner el Numero de Dunbar como cantidad de nodos en nuestra árbol binario, nos encontramos que nos daba SEIS GRADOS DE SEPARACIÓN.
Hay que considerar que una pequeña variación en el grado de separación produce una gran fluctuación en el número de componentes del conglomerado.
¿Es posible esto? ¿Podría explicar el rebuscado Número 147,8 del antropólogo Dunbar? Parecería que sí.
En nuestro modelo de conglomerado consideramos relaciones directas de todos con todos, por lo que Ego puede sostener solo 147,8 otros nodos desde un árbol binario, que por otro lado es la manera mas eficiente de llegar desde Ego al conjunto de punteras de árbol. En esa progresión, la velocidad de trasmisión aumenta a la potencia de 2, a medida que se van abriendo las rama. Lo que justificaría el número, ya comprobado por Milgram, Watts – Strogartz, y Microsoft en poblaciones del orden de los miles de millones de agentes participantes. Hay una relación entre el Número de Dunbar y los seis grados de separación de una red personal. También al ser una red Power Law es explicable que el número seis pueda repetirse en escala mayores ya que las Power Laws son redes independientes de la escala. Tesis que queda como propuesta comprobar si en diferentes redes sociales humanas de distinto tamaño el grado típico de separación sigue siendo seis. Por lo pronto para los casos citados sí se está cumpliendo, no se cumple para Internet, o para las redes de los matemáticos ( red de Erdos), pero estas son redes muy especiales.
Solamente queremos terminar enunciando las propiedades que emergen de este tipo de redes independientes de la escala las Scale Free Networks
foto http://hep.ucsb.edu/courses/ph6b_99/0111299sci-scaling.html
1. Las redes de Libres de Escala tienen distribuciones del tipo Power Law.2. Las redes de Libres de Escala se pueden generar a partir de cierto proceso aleatorio, de los cuales se destaca la agregación por preferencia (opción).
3. Las redes de Libres de Escala están fuertemente conectadas a concentradores (hubs) que las mantienen unidas y les dan robustez aunque fragilidad ante la tolerancia a fallos
4. Las redes de Libres de Escala son genéricas en el sentido que se preservan ante un posible rearmado aleatorio.
5. Las redes de Libres de Escala presentan autosimilitudes.
6. Las redes de Libres de Escala son universales en el sentido de que no dependen de un dominio específico ni del tiempo.
Fuente: Towards a Theory of Scale-Free Graphs: Definition, Properties, and Implications
Lun Li, David Alderson, John C. Doyle, and Walter Willinger
http://www.internetmathematics.org/volumes/2/4/willinger.pdf




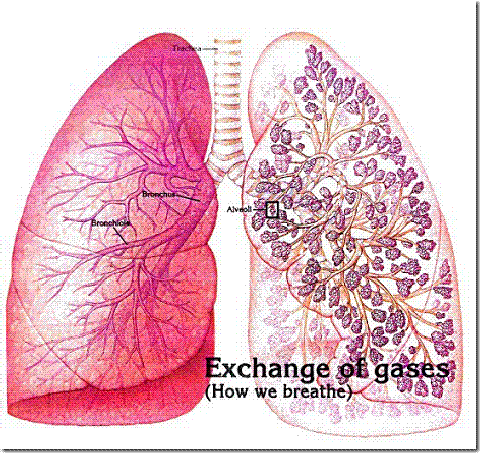


















































4 nos acompañaron:
More info and news about Constructal theory can be found on www.constructal.org
Constructal Twitter feed: http://twitter.com/constructal
http://www.corodebabel.com.ar/Sistemas-Dinamicos-Caoticos/ergodicidad-sistemas-dinamicos-y-otras-yerbas-primera-parte.html ya no existe.
http://www.corodebabel.com.ar tampoco
http://carlosboyle.blogspot.com.ar/2009/02/ergodicidad-for-dummyes.html
Acá se rehabía reproducido aquel post
Publicar un comentario