Pareto vs Gauss 2

Cab Guy e Incencio chicanean el artículo del post anterior. SI saben de estadística les pido que aporten, toda ayuda en ese sentido es bienvenida . Hace unos años publicábamos en El siglo de la Fraternidad el siguiente apartado, hoy veo que hay algunos conceptos confusos debidos a que se toma la curva como un continuo y no como pequeñas porciones discretas que se concentras en pequeños clusters

Power Laws

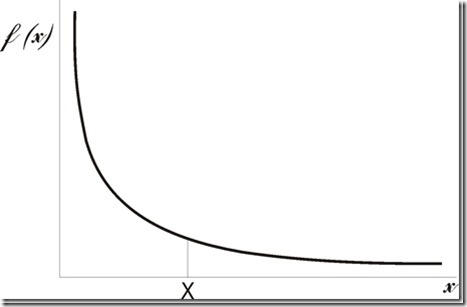
Recordemos la forma de una power law

"Las power laws son las características generales emergentes que presentan los sistemas complejos”.

Citado por Peter Winiwarter de The fractal nature of nature: power laws, ecological complexity and biodiversity- James H. Brown, et all en el capítulo mencionado.

“A pesar de la complejidad y de la idiosincrasia de los organismos y ecosistemas en que se producen, hay aspectos en la estructura y en las funciones de estos sistemas que se mantienen auto-similares, o casi, dentro de una amplia gama de escalas espaciales y temporales. Leyes potenciales empíricas describen matemáticamente una jerarquía de tipo fractal en la organización de estos sistemas”. […]“Por otra parte, mecanismos sencillos que limitan la estructura y la dinámica a mayor escala, también establecen grandes limitaciones sobre cómo los componentes interactúan y se vinculan a gran escala, los sistemas complejos. Juntos, estos mecanismos de abajo para arriba y de arriba para abajo dan lugar a Power Laws y otras características emergentes".

Las power laws son, en consecuencia, las que mantiene autosimilitud a media que el sistema evoluciona y esto puede interpretarse gráficamente como la evolución que presenta un fractal a medida que se va autogenerando.

El tercer elemento que queríamos introducir referente al tema que nos compete en este capítulo es la jerarquía fractal. Llamaremos jerarquía fractal al ordenamiento emergente propio de una Power Law. Si a una power law le corresponde un fractal es evidente que podemos interpretar a las power laws como sistemas evolutivos en el tiempo que por ser fractales se crean de una matriz y evolucionan en un sentido tal que su complejidad aumenta, y a medida que lo hacen, van generando nuevas generaciones emergentes de orden superior a la anterior. Este proceso de desarrollo fractal establece una concurrencia.

Determinado un X cualquiera en el eje de ordenadas, a las x que están a la derecha de X le corresponderán f(x) menores (mayores) que a X, en consecuencia a las que se encuentren a su izquierda le corresponderán f(x) mayores (menores). Así se establece un ordenamiento de mayor a menor o de menor a mayor propio de la distribución muestral de la que se trate, la pendiente de la recta de su representación doble logarítmica, nos dará una idea de cuan diferentes son entre sí los sucesivos muestreos y cuan disímil será la distribución como conjunto. A mayor pendiente de la recta doblelogarítmica mayor será la jerarquía fractal entre sus elementos primitivos. Cuanto mayor sea su dimensión fractal más rápido será el crecimiento de sus partes al aumentar el factor de aumento.

Pero para verlo mejor gráficamente vamos tomar una porción de la curva y la vamos a amplificar en un sector correspondiente al vecindario de X (Δx).

 

Para cualquier x encontraremos una porción de la curva f(x) tal que en un entorno Δx, f(x) decrece (crece) desde a hasta b. En dicho Δx encontramos un Δy= f(a)- f(x) (zona amarilla de la figura) que tendrá un valor opuesto a otro Δy= f(b)- f(x) (zona naranja de la figura), representado en la figura por flechas de sentido opuesto.

Esto es fundamental ya que siempre que se pretenda reunir una diversidad social, tal que su dispersión sea Δx, se establecerá una tensión interna que dependerá de la forma propia de la curva y del sector donde se tome el Δx. Habrá una concurrencia mayor a un lado del Δx que al otro

La diversidad Δx está sujeta a una tensión intrínseca que se provoca a partir del desequilibrio propio de la disponibilidad que representa y que el sistema social en cuestión demanda para vivir, para ello deberá resolver sus diferencias internas para que las disponibilidades en disputa alcancen para todos y a partir de ellas puedan convivir y sostenerse en el tiempo. Esta tensión opuesta y de magnitud relativa al sector de la curva en cuestión, provoca un momento cinético que produce la movilidad social necesaria para que este diferencial pueda evolucionar en un sentido o en otro. Es por eso que ese sistema social lo resuelve, como dice Juan Urrutia Elejalde al describir el concepto de Fraternidad, como una conveniencia de los agentes en la búsqueda de un equilibrio de sus necesidades dentro de la red: "cada hermano está dispuesto a no ser el más listo para permanecer unido a su hermano". El Δy es el máximo esfuerzo que cada agente estará dispuesto a hacer en favor de la cohesión social.

Para que un ser humano (agente de una red de interacción directa) pueda hacer sustentable su vida necesitará reunirse con un grupo social para que en conjunto colaboren en la empresa creadora que es la vida. Esta reunión pone de manifiesto rasgos y necesidades comunes que concurren hacia una demanda también común de esas mismas disponibilidades, lo que de por sí configura un conflicto. Al estar las disponibilidades determinadas por el entorno, el grupo social tiene como única alternativa organizarse internamente en función de esas disponibilidades finitas y ajenas. Esta organización tomará una de estas dos formas: distribución o acopio.

Ahora, si bien siempre existen estas tensiones emergentes propias de cualquier agrupamiento social, el agente deberá optar por un Δx con el cual asociarse; dicho de otra forma elegir el sector de la curva que esté en concordancia con lo que mejor le convenga. Porque hay formas distintas de lograr número ya que en una porción de la curva el número se logra a partir de una gran diversidad, pero con poca tensión social relativa (sector derecho), y en el otro se logra con una gran paridad pero con tensiones sociales debidas a la rivalidad por los recursos mucho mayores.

Si el agente opta por agremiarse a la porción derecha de la curva, esto es minorías muy parejas entre sí en número pero con una gran diversidad, las tensiones internas producidas serán mínimas dado que la curva en ese sector está bastante aplanada. Esto es producto del equilibrio numeral entre los diferentes actores que la hace homogénea numeralmente en la diversidad. La escasa tensión social posibilitará el diálogo y el arreglo racional mediante la implementación de un contrato social.

Por el contrario si tomamos una muestra de la porción izquierda de la curva, a pequeños Δx tendremos una gran tensión social debido a la pronunciada pendiente de la curva en ese sector, en un mismo Δx convivirán sectores con muchas necesidades y otros con muchas menos. Por lo que el agrupamiento social en este sector, para ser equilibrado deberá se muy poco diverso, contrariamente a lo que pasaba en el caso anterior. Este es el caso del populismo: el consenso se logra en base a la casi nula dispersión, a un costo de alto grado de conflictividad latente que da como resultado un equilibrio muy inestable que ante cualquier perturbación puede desencadenar la ruptura social. En este caso la comunicación y el acuerdo social preponderante es esencialmente emocional.

Generalizando, los agrupamiento sociales del sector izquierdo de la curva podrán más numerosos y homogéneos aunque menos estables, los del derecho serán menos numerosos más heterogéneos pero pese a esto más estables. Podemos graficar los casos expuestos mediante dos rectángulos oblongos de superficies equivalentes que contienen el mismo número de agentes cada uno, en el primer caso el rectángulo se encuentra parado con una pequeña base de sustentación y una gran altura (rectángulo verde), en el segundo caso, el rectángulo yace acostado con su lado mayor como base (rectángulo rojo), es evidente que este segundo rectángulo pese a mostrar una gran diversidad, tiene más posibilidades que sobrevivir que el primero debido a que sus rivalidades internas serán mucho menores.

 

Otra consecuencia de este análisis surge a partir de lo que Luque y Agea definen como Dimensión de inmersión. Conceptuar a los sistemas sociales como sectores estancos (Δx fijos) es un error, porque si bien en general las power laws son discretas y no una línea continua como las dibujadas, los agrupamientos discretos están sujetos a una movilidad ascendente o descendente en la curva. De allí la dimensión inmersa se yergue como una propiedad fundamental medible dentro de las power laws.